The exploration of quantum mechanics has reached a pivotal moment, where advanced computational methods intersect with quantum resource understanding. A notable contribution comes from researchers at Freie Universität Berlin, University of Maryland, the National Institute of Standards and Technology (NIST), Google AI, and Abu Dhabi, who have embarked on a mission to uncover Hamiltonian parameters relevant to bosonic excitations in superconducting quantum simulators. Their findings, recently outlined in a preprint on arXiv, promise to pave the way for quantum simulations exhibiting far greater precision than what classical computing can typically offer.
The genesis of this research can be traced to an urgent call received by Jens Eisert, a leading figure in this endeavor. During a conference in Brazil, friends associated with the Google AI project reached out, expressing significant difficulties in calibrating their Sycamore quantum chip. They were specifically struggling with Hamiltonian learning techniques. What initially seemed like a straightforward problem quickly transformed into a complex puzzle, revealing an unexpected challenge in obtaining accurate frequency readings of the Hamiltonian operator.
Eisert assembled a team of skilled Ph.D. students, amongst them Ingo Roth, Dominik Hangleiter, and later Jonas Fuksa, navigating the intricate landscape of Hamiltonian dynamics. The road ahead proved to be arduous, extending over several years, as elucidating the precise Hamiltonian frequencies remained an uphill task amidst the complexities of experimental data.
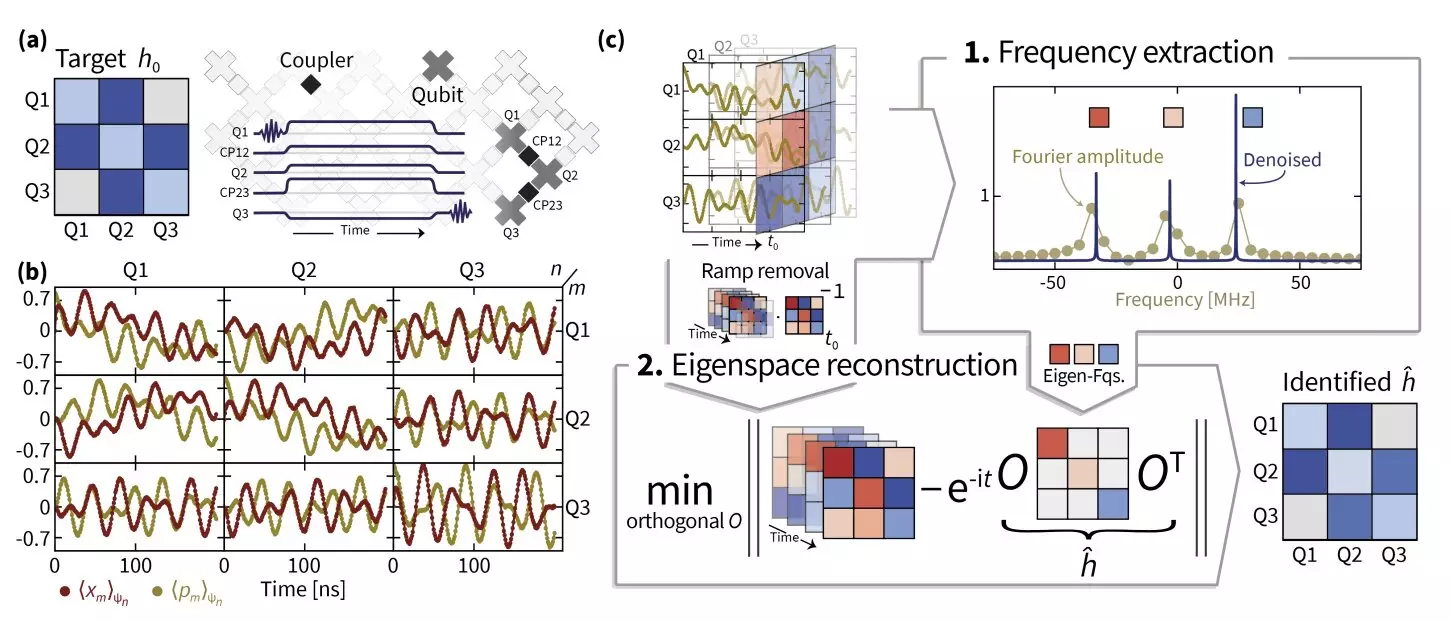
The researchers developed a multi-faceted approach to tackle the problem, rooted in sophisticated methodologies like superresolution and manifold optimization. Superresolution techniques enhanced the precision of eigenvalue estimation, enabling the team to glean accurate Hamiltonian frequencies. Following this, manifold optimization facilitated the recovery of eigenspaces associated with the Hamiltonian operator, bridging the gap towards accurately identifying the Hamiltonian itself.
Manifold optimization is particularly intriguing as it deals with variables residing in complex, curved spaces rather than traditional Euclidean representations. This is crucial in quantum mechanics, where the relationships between variables can be highly non-linear and interdependent, revealing layers of complexity imperative for robust quantum computations.
Eisert also shed light on the nuances of Hamiltonian switching processes, which are inherently imperfect. The quest for a precise fit of Hamiltonian evolution can lead to erroneous interpretations if the underlying processes are not purely Hamiltonian. This research emphasizes the critical importance of accurate signal processing methods, which led to the development of TensorEsprit—an innovative technique that the team harnessed for robust Hamiltonian recovery, even for large-scale systems.
Their findings have far-reaching implications, particularly as the researchers demonstrated the capability to identify Hamiltonian parameters for systems comprised of up to 14 coupled superconducting qubits, effectively utilizing two Sycamore processors. As they delved deeper, they encountered the inherent difficulties of translating Hamiltonian learning techniques into pragmatic applications, shedding light on the sparse literature surrounding this domain. These insights raised pertinent questions about the empirical nature of Hamiltonian parameters, prompting future inquiries into their precise identification through experimental data.
Eisert and his team’s future directions include applying their novel techniques to interconnected quantum systems and exploring the potential of tensor networks within cold atomic frameworks, a concept initially put forth by physicist Immanuel Bloch. Their dedication to advancing this field stems from the notion that a comprehensive understanding of what constitutes a Hamiltonian in a quantum system is crucial for effective predictive capabilities—central to the application of quantum mechanics across varied domains.
The advancements presented by Eisert and his collaborators signify a meaningful stride towards bridging theoretical insights and practical applications in quantum computing. By refining the understanding of Hamiltonian dynamics and proposing methodologies to derive robust quantum simulations, their work holds the potential to unlock new avenues in quantum technology development. As the researchers continue to refine these techniques and explore their implications, the realm of analog quantum simulation promises to emerge as a rich landscape for groundbreaking discoveries, offering fresh perspectives on complex quantum systems and materials.